学習ノート - ゼロから作るDeep Learning

備忘録、殴り書き

3

損失、正解ではない、確率の話。

3.2 活性化関数

ステップ関数では微分できない -> 学習できない。

3.3.2 行列の内積

np.ndim(A) ... 配列の次元数
A.shape ... (行, 列)

>>> A = np.array([[1,2], [3, 4], [5,6]]) 
>>> A.shape
(3, 2)
>>> B = np.array([7,8])
>>> B.shape
(2,)
>>> np.dot(A, B)
array([23, 53, 83])

3.4.2 各層における信号伝達の実装

「人工知能と黒魔術」（視点・論点）
深層学習の非常に簡単な説明
アフィン変換とは - 大人になってからの再学習
ニューラルネットワーク、多様体、トポロジー - Qiita

　式 3.9 A = XW + B の意味がわかる記事。
　ちゃんと理解できてるわけじゃないけどすごい。

　① 内積 = 類似度（って理解でいいんだっけか...）
　　　単純にコサイン類似度なら話はわかるんだけど...

　② 線形変換を繰り返している。
　　　これは分類を用意にしている。

4. ニューラルネットワークの学習

4.2.2 交差エントロピーってなんや

交差エントロピーの導出 -

損失関数は、直感的には理解しづらい。なんでこんなもの採用するんだろうと思ったけど、5.6.3 で Softmax-with-Loss レイヤとして実装した時に、その後方誤差伝搬が t - y と言う簡単かつ直感的に理解しやすい式が出てくる。ただ、実際に二乗和誤差と比較して性能的にいいのか悪いのかはわからない。

4.3.3. 偏微分, 全微分

偏微分は断面
全微分は断面を合わせたベクトル
大学の頃やったなーというのを振り返りながらの、イメージ付け。

のグラフ

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np

"""
>>> x[0]
array([[-3. , -2.9, -2.8, ...,  2.7,  2.8,  2.9],
       [-3. , -2.9, -2.8, ...,  2.7,  2.8,  2.9],
       [-3. , -2.9, -2.8, ...,  2.7,  2.8,  2.9],
       ..., 
       [-3. , -2.9, -2.8, ...,  2.7,  2.8,  2.9],
       [-3. , -2.9, -2.8, ...,  2.7,  2.8,  2.9],
       [-3. , -2.9, -2.8, ...,  2.7,  2.8,  2.9]])

>>> x[1]
array([[-3. , -3. , -3. , ..., -3. , -3. , -3. ],
       [-2.9, -2.9, -2.9, ..., -2.9, -2.9, -2.9],
       [-2.8, -2.8, -2.8, ..., -2.8, -2.8, -2.8],
       ..., 
       [ 2.7,  2.7,  2.7, ...,  2.7,  2.7,  2.7],
       [ 2.8,  2.8,  2.8, ...,  2.8,  2.8,  2.8],
       [ 2.9,  2.9,  2.9, ...,  2.9,  2.9,  2.9]])
"""

x0 = np.arange(-3, 3, 0.1)
x1 = np.arange(-3, 3, 0.1)

# x = np.vstack((x1, x2))
x = np.meshgrid(x0, x1)


print(x)
# x0 = x0.flatten()
# x1 = x1.flatten()

# x = np.array([x0, x1]).T
# x = np.array([x0, x1])

print(x)

def f(x):
  # mesh grid には使えない。
  # return np.sum(x**2)
  return x[0]**2 + x[1]**2

y = f(x)
# x = x.T

# print(y)

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(x[0], x[1],  y)
plt.show()

4.4 勾配 P.104

numerical_gradient を自作
numpy の動作確認も兼ねて。

import numpy as np                                                              
                                                                                
def numerical_gradient(f, x):                                                   
                                                                                
  h = 1e-4 # 0.0001                                                                                           
  grad = np.zeros_like(x)                                                       
                                                                                
  it = np.nditer(x,
    flags=['multi_index'],
    op_flags=['readwrite'])
  
  while not it.finished:                                                        
    i = it.multi_index                                                          
                                                                                
    h_i = np.zeros_like(x)                                                        
    h_i[i] = h                                                             
                                                                                
    grad[i] = (f(x+h_i) - f(x-h_i)) / (2*h)                                     
                                                                                
    it.iternext()                                                               
                                                                                
  return grad


# 関数が返す値は１次元でなければならない。
# grad[i] = np.array([3, 4]) はできないから
def f(x):
  return np.sum(x**2)


# dtype=float を忘れないこと
numerical_gradient(f, np.array([2], dtype=float))

4.4 勾配 P. 111 class simpleNet

>>> def f(W):
>>>   return net.loss(x, t)
>>> 
>>> dw = numerical_gradient(f, net.W)

一瞬？ってなった式。f って x, t が定まっているのだから、これもう完全に定数でしょ、微分なんかできないんじゃないの？って思った。

○ numerical_gradient(f, net.W) が、やっていること
net.W に対して微分。
関数 f の引数 W に対して微分をしていない。

○ ポイント
関数 f の中にある net.loss 関数が参照している net.W と
関数 numerical_gradient に代入されている net.W は同じもの。

5

計算グラフの考え方: 計算グラフは各ノードから１増減させたら、どれだけ増減するかがわかる。即ち微分の値である。

計算グラフを一言で言えば各ノードで１増やした時に、次のノードにはどれだけ値が大きくなるかがわかる。

5.3.3 リンゴの例

疑問: なぜ先頭から 1 が返されるのかがわからなかった。
答え: 後ろの × ノードで値が 1 増えたら、 1 増えるという意味。

総額を a とした時、a が 1 増えたら 1 円増えるという意味。

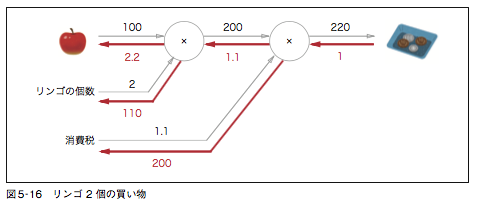
また [リンゴの個数 x リンゴの価格] が１増えた時に、[総額 a] の値がどれだけ増加するかと言えば 1.1 になる。この値が先頭の × ノードの赤字の 1.1 に該当。

5.6.1 Affine レイヤ

Affine 変換の誤差逆伝播法の導出 -

6

6.1 パラメータの更新

6.1.4 Momentum

別の問題について考えて見る。

AdaGrad
利点: 早々に解が得られる。
欠点: 局所解に陥りやすい。

Momentum
前提: 急激な損失関数の降下を見せる箇所では、さらなる降下が期待できる。
利点: 局所解に陥りづらい。
欠点: 運動量が失われないので、振り子のようにいつまで立っても安定することがない。

Adam
AdaGrad と Momentum の中間。

6.2.2. 隠れ層アクティベーションの分布

たぶん入力 x の分布も掲載した方が理解が早い気がする。

Sigmoid 関数について
特徴: 0, 1 に偏りやすい。

図6-10 なぜ 0 と 1 の両極端に別れるんや？と思ったけど、そもそも sigmoid 関数自体がそう言う 0 か 1 を出すような関数なので当然といえば、当然。0 近辺なら基本的に 0.5 に近い値で分布するので納得。

6.2.3 ReLU の場合の重みの初期値

特徴: 0 が多い。

Sigmoid 関数を使った時に比べて極端に 0 の個数が多い。これは ReLU 関数の特性を考えれば理解できる。つまり x < 0 なら y = 0 と言う式である。Sigmoid 関数なら x < 0 でも正の値が帰ってくる。ReLU の場合 x < 0 なら一括して 0 になるので 0 の個数が圧倒的に増えるのはわかる。

w の標準偏差が小さいと、積和 dot を計算すると 0 に近い値になってしまい、回数を重ねるごとに 0 に近づいていく。

また w の標準偏差が大きいと、x*w をした時に w の方が影響が大きくなる。すると正負の振り幅が大きくなり y < 0 となる数が増えてしまい ReLU 関数で 0 にされてしまう。

He の初期値がどのようにして求められたのかわからないが、x*w をした時にバランスよく前の層と同じくらいの大きさの数、入力の値 x - 出力の値 y がプラスマイナス 0 になるように、0 とは言わないまでも同じような数が出力されるようである。なんとなくの理解はこんな感じです。

7

結構基本的な用語がわからなくて詰む。

チャネル ... 何枚の画像を重ねているか。例えば RGB 形式ならば R 赤の画像, G 緑の画像, B 青の画像の 3 チャネル。つまり赤、緑、青の３枚の画像を重ね合わせて１枚にしている。

MNISTのデータは白黒画像なので入力画像は1チャネルになる。もし入力がカラー画像のときはRGBの3チャネルである。

Theanoによる畳み込みニューラルネットワークの実装 (1) - 人工知能に関する断創録

フィルタ ... よく、わからない... フィルタと同じ形状の部分に反応し抜粋し該当箇所に高得点を与えるようなもの？もう少し、各層でどういう処理が行われているのか、見るべきか。でも下記の記事と合わせてなんとなく理解できたような気がする。

CNN
畳み込みニューラルネットワークの仕組み | コンピュータサイエンス | POSTD

各々の層の意味合いを理解できていないので、どうやって各層を繋ぎ合わせるのかという発想に行き着けないでいる。