さわって覚える Python で二分探索木
二分探索木とは
「「左の子孫の値 ≤ 親の値 ≤ 右の子孫の値」という制約を持つ二分木である。
探索木のうちで最も基本的な木構造である。」だ、そうです。
2分探索木, Binary Search Tree - Wikipedia
メリット
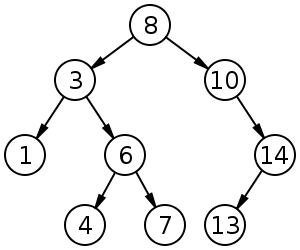
二分探索木は値の探索、データの検索を高速にします。 例えば 6 というデータを探すときに 8 -> 3 -> 6 と辿ればすぐに目的のデータが見つかります。
デメリット
木が片方に偏ってしまう場合があります。 そのような場合は、リストと検索効率が変わらなくなってしまいます。
応用
二分探索木を応用した B 木 B-tree などはデータベースの世界で活用されています。 二分探索木は、木というデータ構造の基礎になるものです。
この対数化を実現しているのが、実はSQLのインデックスで使われている B-tree というアルゴリズムで、 このインデックスがあるがゆえに、 テーブルの行数が10倍、1万倍、1億倍になっても性能は1億分の1ではなく8分の1ぐらいのおだやかな性能劣化で収まるのです。 こういう圧倒的なパワーこそがサイエンスと呼ぶにふさわしいものです。
MongoDBの様なNoSQLに勢いがあるのは何故ですか?SQLと比べてどんな利点や欠点がありますか?
サンプルコード(とりあえず、さわってみよう)
実装した二分探索木のコードになります。
binary_search_tree - GitHub
とりあえず、ダウンロードして、さわってみましょう。 ちょっとでも理解できるように、木を表示する log.output 関数を用意しました。
以下は、サンプルコードです。search は、ちょっとわかりづらいですね...。
import binary_search_tree import log # # 1. 挿入 insert # 上の図と同じ木を作る。 # bst = binary_search_tree.BinarySearchTree() bst.insert(8) bst.insert(3) bst.insert(1) bst.insert(6) bst.insert(10) bst.insert(4) bst.insert(7) bst.insert(14) bst.insert(13) print(log.output(bst)) # 08 # 03 10 # 01 06 14 # 04 07 13 # # 2. 探索 search # # 省略 try: bst.search(7) except ValueError: print('The data doesn\'t exist.') else: print('The data exists') # The data exists try: bst.search(9) except ValueError: print('The data doesn\'t exist.') else: print('The data exists') # The data doesn't exist. # # 3. 削除 delete # 削除には2種類方法があります。 # 3.1. delete_left ... 左の子の最大値をルートに持ってくる bst.delete_left(8) print(log.output(bst)) # 07 # 03 10 # 01 06 14 # 04 13 # 3.2. delete_right ... 右の子の最小値をルートに持ってくる bst.delete_right(7) print(log.output(bst)) # 10 # 03 14 # 01 06 13 # 04 # # 4. 整列 list # # 4.1. 再帰による実装 print(bst.list()) # [1, 3, 4, 6, 10, 13, 14] # 4.2. 再帰でない実装 print(bst.list_sequentially()) # [1, 3, 4, 6, 10, 13, 14]
目次
- 二分探索木の概要を説明します。
- なんでそうやって実装したの?
- 実はリストでも同じことができます。(二分探索とクイックソート)
1. 実装した木の操作 概要
- 挿入 insert
- 探索 search
- 削除 delete
- 整列 list
1. 挿入, insert
8, 3, 1, 6, 10, 4, 7, 14, 13 の順番に木に値を挿入してみましょう。
比較的これは簡単です。









2. 探索, search
探索も挿入と同じ考え方なので簡単かなと思います。
3. 削除, delete
ノードの削除の仕方は、2通りあります。「左の木の最大値」を削除する方法と「右の木の最小値」を削除する方法です。
3.0. 元の木

3.1. "8" を削除する
8 を削除するには、どうすれば良いでしょうか?単純に削除しただけではダメで、8 がいた場所に別のノードを持ってこないといけません。 このとき 8 がいる場所にはいることができるノードは 3 ~ 10 の間のノードならはいることができます。
例えば 6 ならどうでしょうか?6 を削除すると、また 6 の場所が空いてしまいます。これは、なんだか面倒くさそうですね。
「左の木の右の木の葉」か「右の木の左の木の葉」を持ってくると、木の再構成がもっも小さくて済みます。例えば 4, 7 は 8 がいた場所はいることができますし、葉から抜けても木を作り直す必要はありません。
どちらでもいいのなら「左の木の最大値」を持ってくると決めうちしてしまいましょう。7 を上に持ってきます。

3.2. "7" を削除する
3 ~ 10 の間にあって葉であるノードは 4 です。4 を持って来れば一番簡単なのですが、ここでは「左の木の最大値」の逆「右の木の最小値」を持ってくることを考えてみましょう。すると 10 が右の木でもっとも大きい値です。
でも安心してください。ノード 14 を上に持って来ればいいだけです。

3.3. "3" を削除する

◯ 実装されていない delete の処理
ネットに転がっている二分探索木のコードは、削除のコードが実装されていないか、 あるいはこのような言い方はよくないと思うのですが若干煩雑なコードになっています。
実装されていないのは、削除のコードが挿入、探索、整列よりも複雑だから。 また、あったとしても、若干複雑なのは、たいていの場合、削除を実装するためにノードに 親 parent への参照を属性に保存させているから。 二分探索木について言えば、複雑になるのを回避するには実は parent を持たせないほうが良かったりします。
parent を持たせずに、削除をどうやって実装するか? それを実装するには、削除後の root のノードを返すように実装すると上手くいきます。
削除の実装にあたって、参考にした神様のサイト
削除の実装に当たって、次のサイトを参考にしました。
削除した木のルートを返すと色々と上手くいくことを学びました。
Algorithms with Python - 二分木 (binary tree) とヒープ (heap)
4. 整列, list
二分探索木はソートされたリストを簡単に生成することができます。2つの実装の仕方があるかなと思っています。1つ目は再帰処理。もう1つは順次処理。すいません、作図が追いつかないので、コードで説明します。
4.1. 再帰処理 ... 木を潰して平らにするイメージ
再帰処理で簡単にソートされたリストにすることができます。木を潰して平らにすると自動的にソートできるイメージです。 って言われても、わからないですよね...。 Javascript, CSS アニメーションで作ってみたい...
def BinarySearchNode(object): ... def list(self): if self.left: left_sorted_list = self.left.list() else: left_sorted_list = [] center = self.value if self.right: right_sorted_list = self.right.list() else: right_sorted_list = [] return left_sorted_list + [center] + right_sorted_list
4.2. 順次処理 ... 1つずつ探す
再帰に依らない方法は、あるのでしょうか?1つずつ値を取り出すことはできるのでしょうか?
def BinarySearchNode(object): ... def list_sequentially(self): sorted_list = [] path = Path(self) # 例外 StopIteration が起こるまで # next 次の値を取り続ける while True: try: value = next(path) except StopIteration: break else: sorted_list.append(value) return sorted_list
結構簡単に実装できます。考え方は「次に大きな値を探す」です。次の2つの操作を繰り返します。
- 右下に木があれば、右下の木の最小値を見つける。
- 右下に木がなければ、右上の親を探す。
next(path) は、path.__next__() を呼び出しています。なぜ、このような面倒なことをしているかは、追って説明します。
class Path(object): def __init__(self, root): pseudo_node = BinarySearchNode(None) pseudo_node.right = root self._route = [pseudo_node] def __next__(self): # 1. 右下に木があれば、右下の木の最小値を見つける。 if self._current_node().right: self._seek_right_min() # 2. 右下に木がなければ、右上の親を探す。 else: self._seek_right_parent() return self._current_node().value def _seek_right_min(self): self._route.append(self._current_node().right) while self._current_node().left: self._route.append(self._current_node().left) def _seek_right_parent(self): try: while self._route.pop() == self._current_node().right: pass except IndexError: raise StopIteration def _current_node(self): return self._route[-1] def __iter__(self): return self
◯ 深さ優先探索
順次で要素を取り出す時に経路の辿る方法は「深さ優先探索」になります。
深さ優先探索と幅優先探索 - 高校数学の美しい物語
2. 実装の方針
よく見かける二分探索木のサンプルコードには、大きく分けて次のような違いがあります。 ここでは、何故、今回このように実装したかについて説明します。
- Node だけ実装しているものと、Tree と Node を実装しているもの。
- 親への参照 parent を持っているものと、持っていないもの。
- while 文で実装されているものと、再帰で実装されているもの。
1. BinarySearchTree クラスと BinarySearchNode クラスの2つに分けるか、それとも分けないか。
BinarySearchTree クラスと BinarySearchNode クラス を分けるのは実装が面倒です。
しかし、空の木を表現するときにどうしても必要になります。
これは特に削除 delete の機能を実装する場合に、必要性が顕著になります。
1.1. 空の木を、表現するため
空の木をどうやって、表現しますか?
もし BinarySearchTree クラスと BinarySearchNode クラスをわけなかった場合、どうやって要素を持たない木を表現しますか? それには2つのやり方があると思います。
代替案 1: None
1つ目は None を値を持たない木であるとすることです。
しかしそうすると、1度、木が空に None になってしまうと、もう木という型ではなくなってしまいます。
結果的に insert, list と言った処理が実行できなくなります。
from binary_search_tree import * # 木を生成する。 bst = BinarySearchNode(8) bst.insert(3) bst.insert(1) bst.insert(6) bst.insert(10) bst.insert(4) bst.insert(7) bst.insert(14) bst.insert(13) # 木を空にする。 # 削除すると根が変わるので # 削除のたびに代入しないといけない。 bst = bst.delete_left(8) bst = bst.delete_left(3) bst = bst.delete_left(1) bst = bst.delete_left(6) bst = bst.delete_left(10) bst = bst.delete_left(4) bst = bst.delete_left(7) bst = bst.delete_left(14) bst = bst.delete_left(13) # 木を空にすると None になる assert bst is None # もう insert はできない... # AttributeError bst.insert(3)
代替案 2: BinarySearchNode(None)
2つ目は None を値に持つ BinarySearchNode を空の木と見立てることです。
これなら空になっても insert などの処理は実行できそうです。
class BinarySearchNode(object):
# insert メソッドが少しだけ、複雑になるだけで済む。
def insert(self, value):
if self.value is None:
self.value = value
elif value < self.value:
if self.left:
self.left = BinarySearchNode(None)
self.left.insert(value)
else:
if self.right:
self.left = BinarySearchNode(None)
self.right.insert(value)
なんだか上手くいきそうですね。次のことを考えてみましょう。
1.2. ルートを削除したときの対応のため。
削除の操作をした時に、根を変数、属性に代入できれば良いのですが。 2つ以上の変数または属性に木が代入されていると、もう逃げられなくなります。
import binary_search_tree import log # BinsarySearchNode を木に見立てる... bst = binary_search_tree.BinarySearchNode(8) bst.insert(3) bst.insert(1) bst.insert(6) bst.insert(10) bst.insert(4) bst.insert(7) bst.insert(14) bst.insert(13) # あるオブジェクトに bst を登録する。 dct1 = {'tree': bst} dct2 = {'tree': bst} print(log.output_node(dct1['tree'])) """ 08 03 10 01 06 14 04 07 13 """ # 8 を削除すると... bst.delete_left(8) # 8 しか表示されない... print(log.output_node(dct1['tree'])) """ 08 """ print(log.output_node(dct2['tree'])) """ 08 """ # これは面倒すぎる... # dct1['tree'] = dct2['tree'] = bst.delete_left(8)
◯ まとめ
空の木を表現するには Node と Tree を分けないといけない。
2. BinarySearchNode の属性に parent を持たせる、それとも持たせない?
削除 delete の処理が、とても複雑になるからです。 特に parent の取り扱いで処理が、とても長くなってパッと見では、わかりづらいコードになります。
Path クラスを実装する際には parent があると、ごく若干わかりやすくなるのですが、 これは、二分探索木の処理を説明するためだけのメソッドで、 本来は不要なので parent を持たせない実装にしました。
いちおう parent を属性にもたせたものも実装しましたが、parent もたせるのはよくないかな.. と。
ファイル名に parent と書かれている方が、それになります。
binary_search_tree_parent.py - GitHub
3. 再帰処理か while 文か?
基本的にはメソッドを再帰処理で処理しました。ただし list_sequentially に関わる処理を除きます。
list_sequentially に関わる処理は while 文でないとかけないので、それとの対比を明確にする意味で、再帰処理で記述しました。
実行速度で言えば、while 文で書いたほうが速いと思います。今回は、学習目的なので再帰処理で記述しました。
3. quick sort と binary search
実は quick sort と binary search で、二分探索木と全く同じことができます。
1. 二分探索 bisect
二分探索木には、どのような利点があるのでしょうか?
二分探索木は、二分木に対して、あるルールを適用することによって、データの探索効率を向上させたデータ構造です。
二分探索木 - Programming Place Plus アルゴリズムとデータ構造編
実は、わざわざ二分探索木を実装しなくても、ソートされたリストを用いて同じことができます。この方法を二分探索と言います。
二分探索 - わくわくアカデミー(鬼のようにわかりやすい)
二分探索 - Wikipedia
実は Python では二分探索を行う bisect と言う組み込みモジュールを提供してくれています。
random_list = [8, 3, 1, 6, 10, 4, 7, 14, 13] sorted_list = sorted(random_list) print(sorted_list) # [1, 3, 4, 6, 7, 8, 10, 13, 14] """ 1. bisect ソートされた順番を崩すことなく 要素を挿入できる。 """ import bisect bisect.insort_left(sorted_list, 11) print(sorted_list) # [1, 3, 4, 6, 7, 8, 10, 11, 13, 14] """ 2. 二分探索木 ソートされた順番を崩すことなく 要素を挿入できる、と考えることもできる。 """ binary_search_tree = BinarySearchTree() binary_search_tree.insert_iterable(random_list) binary_search_tree.insert(11) print(list(binary_search_tree)) # [1, 3, 4, 6, 7, 8, 10, 11, 13, 14]
8.6. bisect 配列二分法アルゴリズム - Python 標準ライブラリ
二分探索木と二分探索は異なるものです。二分探索木はデータ構造です、二分探索はソートされたリストを活用したアルゴリズムです。
二分探索木では平衡状態を保つためには、木の回転の操作などが必要になります。ソートされたリストは平衡状態を保った二分探索木であると考えることもできます。リストを用いた二分探索 bisect を用いれば、平衡状態を保つために木の回転をする必要がありません。
また、bisect モジュールを用いればソートされたリストを高速に検索することもできます。
2. クイックソート
二分探索木を使ったソートは、基本的にはクイックソートと同じことをしています。
クイックソート - わくわくアカデミー(鬼のようにわかりやすい)
クイックソートは、基準になる値を1つ決め、それより大きい値のグループと小さい値のグループに分けます。そしてこの作業を繰り返し、ソートされたリストを得ます。それは、ちょうど二分探索木が、挿入された要素を左側の子と右側の子に振り分ける動作と、とてもよく似ています。
実際、クイックソートのコードは、二分探索木からリストを生成するコードとそっくりです。
def quick_sort(lst): if not lst: return [] # 1. smaller_sorted_list = quick_sort([e for e in lst[1:] if e <= lst[0]]) center = lst[0] bigger_sorted_list = quick_sort([e for e in lst[1:] if e > lst[0]]) # 2. sorted_list = smaller_sorted_list + [center] + bigger_sorted_list # 3. return sorted_list lst = [8, 3, 1, 6, 10, 4, 7, 14, 13] print(quick_sort(lst))
クイックソートは名前の通り、高速にソートを行えます。しかし、データに偏りがあったりすると、高速にソートできません。
そのため Python のソートアルゴリズムには TimSort が実装されているそうです。
高速な安定ソートアルゴリズム "TimSort" の解説
3. ヒープキュー, heapq
- 8.5. heapq ヒープキューアルゴリズム - Python 標準ライブラリ
- ヒープソート - わくわくアカデミー(鬼のようにわかりやすい)
- No.205 マージして辞書順最小 - yukicoder
- heapq を使った回答(2018/07/16 現在最速)
4. Path クラスの正体
実は Path クラスは、イテレータです。 そのため、次のように __iter__ にメソッドを定義すると、なんと for 文で使えるようになります。
from binary_search_tree import BinarySearchTree from binary_search_tree import BinarySearchNode from binary_search_tree import Path bst = BinarySearchTree() for value in 8, 3, 1, 6, 10, 4, 7, 14, 13: bst.insert(value) # Error for value in bst: print(value) # Success BinarySearchNode.__iter__ = lambda self: Path(self) for value in bst: print(value)
では、イテレータとは何でしょうか?実はイテレータとは、for 文そのものです。
for 文とは何かについて、説明していきます。
