１対１の当たり判定、長方形の交差問題

ごく簡単な条件で判定できます。

max(a.x1, b.x1) ≤ min(a.x2, b.x2)
max(a.y1, b.y1) ≤ min(a.y2, b.y2)

def has_intersect(a, b):
    return max(a.x1, b.x1) <= min(a.x2, b.x2) \
           and max(a.y1, b.y1) <= min(a.y2, b.y2)

こんな感じで使います。

>>> has_intersect(Rectangle(0,0,10,10), Rectangle(5,5,15,15))
True
>>>
>>> has_intersect(Rectangle(0,0,10,10), Rectangle(15,15,25,25))
False
>>> 

長方形 Rectangle クラス

class Rectangle(object):
    def __init__(self, x1, y1, x2, y2):
        if not is_rectangle(x1, y1, x2, y2):
            raise ValueError("Coordinates are invalid.\n" +
                             "Rectangle" + str((x1, y1, x2, y2)))
        self.x1 = x1
        self.y1 = y1
        self.x2 = x2
        self.y2 = y2

def is_rectangle(x1, y1, x2, y2):
    return x1 <= x2 and y1 <= y2

なんでこんなので判定できるの？式の意味は？

条件式は、交差した長方形の領域が存在するかどうかを判定しています。

Step 1. 1 つの長方形で囲まれた領域

2 点 (x1, y1), (x2, y2) で囲まれた長方形を、点で囲まれた長方形ではなく

ポイント１ 長方形の表現
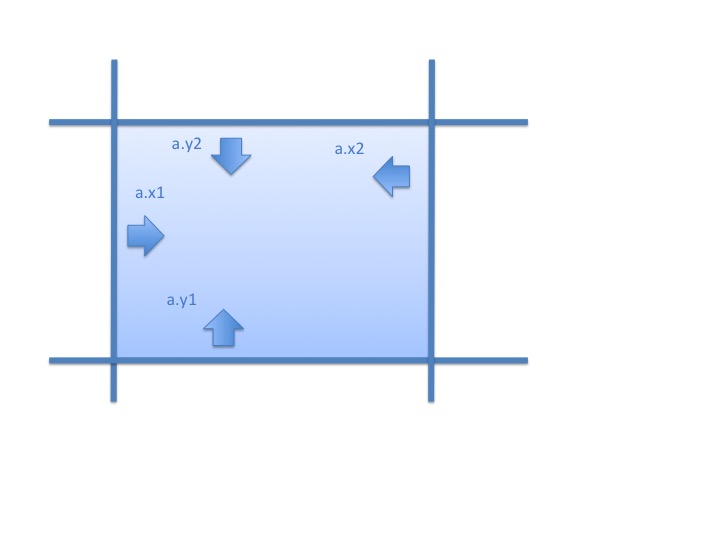
長方形は x1, y1, x2, y2 の 4 つの領域で囲まていると考えることにします。

右方向の領域: x1 ≤ x
上方向の領域: y1 ≤ y
左方向の領域: x ≤ x2
下方向の領域: y ≤ y2

ポイント２ 長方形の条件
x1, y1, x2, y2 の 4 つの領域が重複している箇所があれば
長方形であると言える。

条件を次のように考えることができます。

x1 ≤ x2
y1 ≤ y2

def is_rectangle(x1, y1, x2, y2):
    return x1 <= x2 and y1 <= y2

Step 2. 2 つの長方形で囲まれた領域

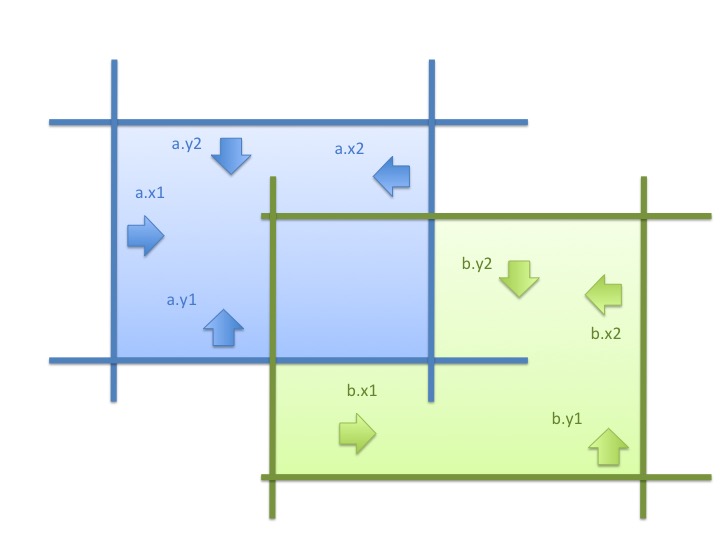
考え方は同じです。上下左右方向の４つの領域が
４つ同時に重なる箇所があるかないかを判定ます。
あれば交差しているし、なければ交差していません。

Step 1 では領域を表現する線は各方向に 1 つだけでした。
ここでは 2 つ存在しています。
交差する領域を探していきます。

右方向の交差する領域: a.x1, b.x1 の大きい方から右方向
上方向の交差する領域: a.y1, b.y1 の大きい方から上方向
左方向の交差する領域: a.x2, b.x2 の小さい方から左方向
下方向の交差する領域: a.y2, b.y2 の小さい方から下方向

右方向の交差する領域: max(a.x1, b.x1) ≤ x
上方向の交差する領域: max(a.y1, b.y1) ≤ y
左方向の交差する領域: x ≤ min(a.x2, b.x2)
下方向の交差する領域: y ≤ min(a.y2, b.y2)

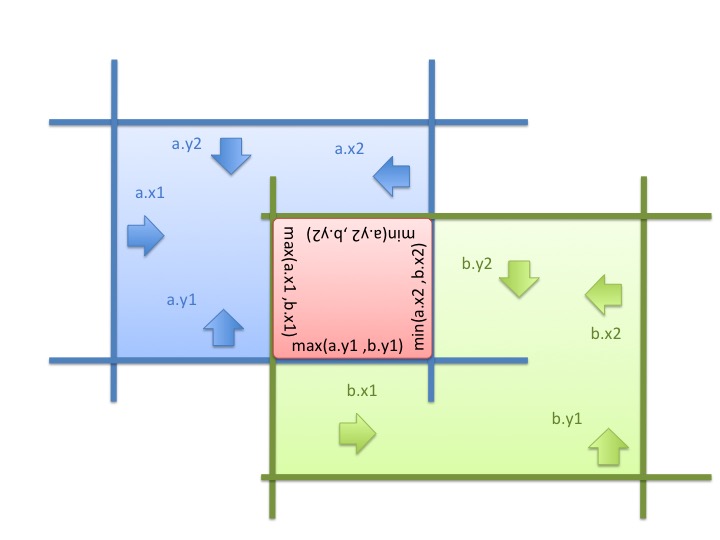
これで４方向の領域がそれぞれ取得できました。あとは Step1 で確認した長方形の条件を当てはめて、交差しているかを確認するだけです。

max(a.x1, b.x1) ≤ min(a.x2, b.x2)
max(a.y1, b.y1) ≤ min(a.y2, b.y2)

def has_intersect(a, b):
    return max(a.x1, b.x1) <= min(a.x2, b.x2) \
           and max(a.y1, b.y1) <= min(a.y2, b.y2)

当てはめてと言われても「え？」ってなると思いますが、こんな感じで is_rectangle 関数を使うと Step1 の条件を当てはめているのがわかります。

def has_intersect(a, b):
    return is_rectangle(intersect_bound(a, b))

def intersect_bound(a, b):
    """4方向の各領域の積集合を求める関数"""
    x1 = max(a.x1, b.x1)
    y1 = max(a.y1, b.y1)
    x2 = min(a.x2, b.x2)
    y2 = min(a.y2, b.y2)
    return x1, y1, x2, y2

交差する領域

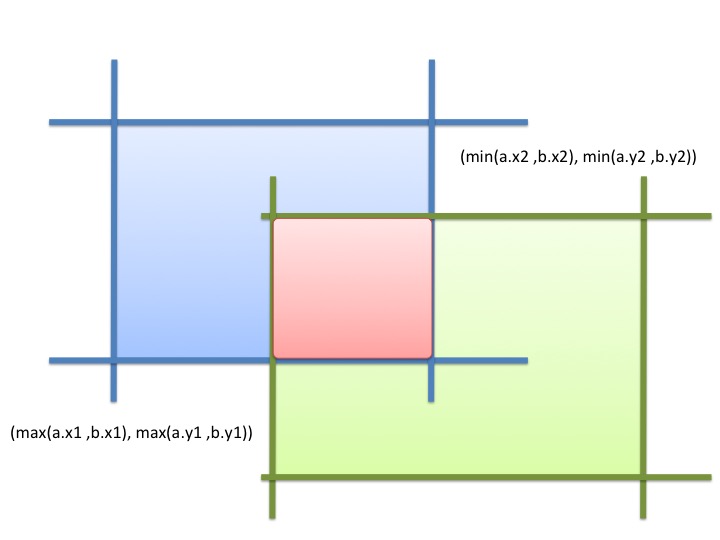
このとき、これは交差する長方形の領域を表現します。

def intersect(a, b):
    return Rectangle(max(a.x1, b.x1), max(a.y1, b.y1),
        min(a.x2, b.x2), min(a.y2, b.y2))

あるいはこんな感じで

def intersect(a, b):
    return Rectangle(intersect_bound(a, b))

>>> intersect(Rectangle(0,0,10,10), Rectangle(5,5,15,15))
Rectangle(5, 5, 10, 10)
>>>

交差していなければ、None ではなく例外を投げる。
『Effective Python』Item 14: Noneを返すよりも例外を発生させよう

>>> intersect(Rectangle(0,0,10,10), Rectangle(15,15,25,25))
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "<stdin>", line 22, in __and__
  File "<stdin>", line 6, in __init__
ValueError: Coordinates are invalid.
Rectangle(15, 15, 10, 10)
>>> 

◯ 実装まとめ

def has_intersect(a, b):
    return is_rectangle(intersect_bound(a, b))


def is_rectangle(x1, y1, x2, y2):
    return x1 <= x2 and y1 <= y2


def intersect(a, b):
    return Rectangle(intersect_bound(a, b))


def intersect_bound(a, b):
    x1 = max(a.x1, b.x1)
    y1 = max(a.y1, b.y1)
    x2 = min(a.x2, b.x2)
    y2 = min(a.y2, b.y2)
    return x1, y1, x2, y2


class Rectangle(object):
    def __init__(self, x1, y1, x2, y2):
        if not is_rectangle(x1, y1, x2, y2):
            raise ValueError("Coordinates are invalid.\n" +
                             "Rectangle" + str((x1, y1, x2, y2)))
        self.x1 = x1
        self.y1 = y1
        self.x2 = x2
        self.y2 = y2

    def __repr__(self):
        return ("Rectangle" + str((self.x1, self.y1, self.x2, self.y2)))